How to use these slides

Viewing slides…

• Press ‘f’ enable fullscreen mode
• Press ‘o’ or ‘Esc’ to enable overview mode
• Pressing ‘Esc’ exits all of these modes.
• Hold down ‘alt’ and click on any element to zoom in. ‘Alt’ + click anywhere to zoom back out.
• Use the Search box (top right) to search keywords in presentation

Printing slides…

• Click here to open a printable version of these slides.
• Right click and print from browser or save as PDF (e.g. Chrome)

A Layered Grammar of Graphics

• Wickham (2010) proposed the Layered Grammar of Graphics, which built upon the original Grammar of Graphics first proposed by Wilkinson (2005).
• The idea was to build a grammar that could describe any data visualisation as succinctly as possible.
• This is a big idea because it allows us to move away from a narrow list of methods, into unlimited possibilities

A Layered Grammar of Graphics

• Wickham proposed that a graphic is a series of layers consisting of…
  • a default dataset and set of mappings from variables to aesthetics,
  • one or more layers, with each layer having - one geometric object - one statistical transformation, - one position adjustment, - and optionally, one dataset and set of aesthetic mappings - one scale for each aesthetic mapping used
  • a coordinate system
  • an optional facet specification.

Layers

• Any graphic can be thought of as a series of layers…

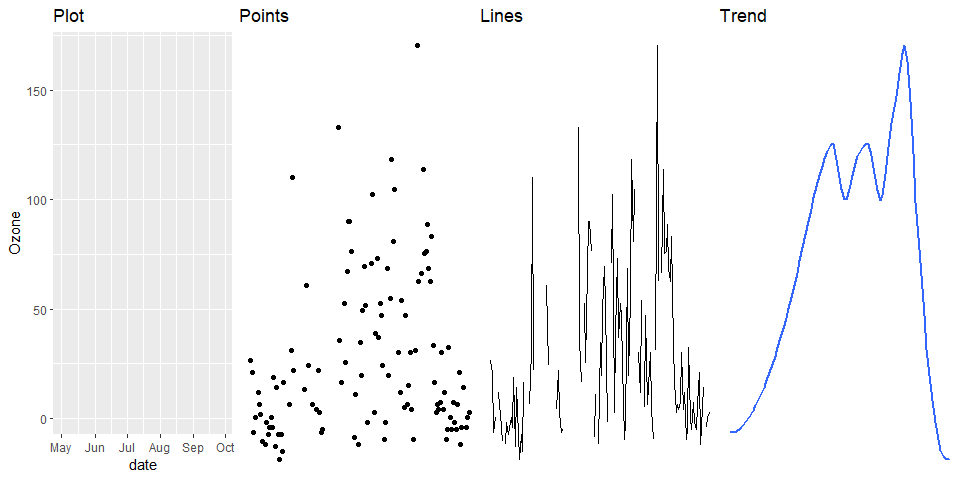
• Put them together and we create a graph…

Layers Cont.

Data

• Layers are composed of data, aesthetic mappings, statistical transformations, geometric objects and optional position adjustments.
• Data are obvious…

##     Ozone Solar.R Wind Temp Month Day       date
## 1      41     190  7.4   67     5   1 1973-05-01
## 2      36     118  8.0   72     5   2 1973-05-02
## 3      12     149 12.6   74     5   3 1973-05-03
## 4      18     313 11.5   62     5   4 1973-05-04
## 5      NA      NA 14.3   56     5   5 1973-05-05
## 6      28      NA 14.9   66     5   6 1973-05-06
## 7      23     299  8.6   65     5   7 1973-05-07
## 8      19      99 13.8   59     5   8 1973-05-08
## 9       8      19 20.1   61     5   9 1973-05-09
## 10     NA     194  8.6   69     5  10 1973-05-10
## 11      7      NA  6.9   74     5  11 1973-05-11
## 12     16     256  9.7   69     5  12 1973-05-12
## 13     11     290  9.2   66     5  13 1973-05-13
## 14     14     274 10.9   68     5  14 1973-05-14
## 15     18      65 13.2   58     5  15 1973-05-15
## 16     14     334 11.5   64     5  16 1973-05-16
## 17     34     307 12.0   66     5  17 1973-05-17
## 18      6      78 18.4   57     5  18 1973-05-18
## 19     30     322 11.5   68     5  19 1973-05-19
## 20     11      44  9.7   62     5  20 1973-05-20
## 21      1       8  9.7   59     5  21 1973-05-21
## 22     11     320 16.6   73     5  22 1973-05-22
## 23      4      25  9.7   61     5  23 1973-05-23
## 24     32      92 12.0   61     5  24 1973-05-24
## 25     NA      66 16.6   57     5  25 1973-05-25
## 26     NA     266 14.9   58     5  26 1973-05-26
## 27     NA      NA  8.0   57     5  27 1973-05-27
## 28     23      13 12.0   67     5  28 1973-05-28
## 29     45     252 14.9   81     5  29 1973-05-29
## 30    115     223  5.7   79     5  30 1973-05-30
## 31     37     279  7.4   76     5  31 1973-05-31
## 32     NA     286  8.6   78     6   1 1973-06-01
## 33     NA     287  9.7   74     6   2 1973-06-02
## 34     NA     242 16.1   67     6   3 1973-06-03
## 35     NA     186  9.2   84     6   4 1973-06-04
## 36     NA     220  8.6   85     6   5 1973-06-05
## 37     NA     264 14.3   79     6   6 1973-06-06
## 38     29     127  9.7   82     6   7 1973-06-07
## 39     NA     273  6.9   87     6   8 1973-06-08
## 40     71     291 13.8   90     6   9 1973-06-09
## 41     39     323 11.5   87     6  10 1973-06-10
## 42     NA     259 10.9   93     6  11 1973-06-11
## 43     NA     250  9.2   92     6  12 1973-06-12
## 44     23     148  8.0   82     6  13 1973-06-13
## 45     NA     332 13.8   80     6  14 1973-06-14
## 46     NA     322 11.5   79     6  15 1973-06-15
## 47     21     191 14.9   77     6  16 1973-06-16
## 48     37     284 20.7   72     6  17 1973-06-17
## 49     20      37  9.2   65     6  18 1973-06-18
## 50     12     120 11.5   73     6  19 1973-06-19
## 51     13     137 10.3   76     6  20 1973-06-20
## 52     NA     150  6.3   77     6  21 1973-06-21
## 53     NA      59  1.7   76     6  22 1973-06-22
## 54     NA      91  4.6   76     6  23 1973-06-23
## 55     NA     250  6.3   76     6  24 1973-06-24
## 56     NA     135  8.0   75     6  25 1973-06-25
## 57     NA     127  8.0   78     6  26 1973-06-26
## 58     NA      47 10.3   73     6  27 1973-06-27
## 59     NA      98 11.5   80     6  28 1973-06-28
## 60     NA      31 14.9   77     6  29 1973-06-29
## 61     NA     138  8.0   83     6  30 1973-06-30
## 62    135     269  4.1   84     7   1 1973-07-01
## 63     49     248  9.2   85     7   2 1973-07-02
## 64     32     236  9.2   81     7   3 1973-07-03
## 65     NA     101 10.9   84     7   4 1973-07-04
## 66     64     175  4.6   83     7   5 1973-07-05
## 67     40     314 10.9   83     7   6 1973-07-06
## 68     77     276  5.1   88     7   7 1973-07-07
## 69     97     267  6.3   92     7   8 1973-07-08
## 70     97     272  5.7   92     7   9 1973-07-09
## 71     85     175  7.4   89     7  10 1973-07-10
## 72     NA     139  8.6   82     7  11 1973-07-11
## 73     10     264 14.3   73     7  12 1973-07-12
## 74     27     175 14.9   81     7  13 1973-07-13
## 75     NA     291 14.9   91     7  14 1973-07-14
## 76      7      48 14.3   80     7  15 1973-07-15
## 77     48     260  6.9   81     7  16 1973-07-16
## 78     35     274 10.3   82     7  17 1973-07-17
## 79     61     285  6.3   84     7  18 1973-07-18
## 80     79     187  5.1   87     7  19 1973-07-19
## 81     63     220 11.5   85     7  20 1973-07-20
## 82     16       7  6.9   74     7  21 1973-07-21
## 83     NA     258  9.7   81     7  22 1973-07-22
## 84     NA     295 11.5   82     7  23 1973-07-23
## 85     80     294  8.6   86     7  24 1973-07-24
## 86    108     223  8.0   85     7  25 1973-07-25
## 87     20      81  8.6   82     7  26 1973-07-26
## 88     52      82 12.0   86     7  27 1973-07-27
## 89     82     213  7.4   88     7  28 1973-07-28
## 90     50     275  7.4   86     7  29 1973-07-29
## 91     64     253  7.4   83     7  30 1973-07-30
## 92     59     254  9.2   81     7  31 1973-07-31
## 93     39      83  6.9   81     8   1 1973-08-01
## 94      9      24 13.8   81     8   2 1973-08-02
## 95     16      77  7.4   82     8   3 1973-08-03
## 96     78      NA  6.9   86     8   4 1973-08-04
## 97     35      NA  7.4   85     8   5 1973-08-05
## 98     66      NA  4.6   87     8   6 1973-08-06
## 99    122     255  4.0   89     8   7 1973-08-07
## 100    89     229 10.3   90     8   8 1973-08-08
## 101   110     207  8.0   90     8   9 1973-08-09
## 102    NA     222  8.6   92     8  10 1973-08-10
## 103    NA     137 11.5   86     8  11 1973-08-11
## 104    44     192 11.5   86     8  12 1973-08-12
## 105    28     273 11.5   82     8  13 1973-08-13
## 106    65     157  9.7   80     8  14 1973-08-14
## 107    NA      64 11.5   79     8  15 1973-08-15
## 108    22      71 10.3   77     8  16 1973-08-16
## 109    59      51  6.3   79     8  17 1973-08-17
## 110    23     115  7.4   76     8  18 1973-08-18
## 111    31     244 10.9   78     8  19 1973-08-19
## 112    44     190 10.3   78     8  20 1973-08-20
## 113    21     259 15.5   77     8  21 1973-08-21
## 114     9      36 14.3   72     8  22 1973-08-22
## 115    NA     255 12.6   75     8  23 1973-08-23
## 116    45     212  9.7   79     8  24 1973-08-24
## 117   168     238  3.4   81     8  25 1973-08-25
## 118    73     215  8.0   86     8  26 1973-08-26
## 119    NA     153  5.7   88     8  27 1973-08-27
## 120    76     203  9.7   97     8  28 1973-08-28
## 121   118     225  2.3   94     8  29 1973-08-29
## 122    84     237  6.3   96     8  30 1973-08-30
## 123    85     188  6.3   94     8  31 1973-08-31
## 124    96     167  6.9   91     9   1 1973-09-01
## 125    78     197  5.1   92     9   2 1973-09-02
## 126    73     183  2.8   93     9   3 1973-09-03
## 127    91     189  4.6   93     9   4 1973-09-04
## 128    47      95  7.4   87     9   5 1973-09-05
## 129    32      92 15.5   84     9   6 1973-09-06
## 130    20     252 10.9   80     9   7 1973-09-07
## 131    23     220 10.3   78     9   8 1973-09-08
## 132    21     230 10.9   75     9   9 1973-09-09
## 133    24     259  9.7   73     9  10 1973-09-10
## 134    44     236 14.9   81     9  11 1973-09-11
## 135    21     259 15.5   76     9  12 1973-09-12
## 136    28     238  6.3   77     9  13 1973-09-13
## 137     9      24 10.9   71     9  14 1973-09-14
## 138    13     112 11.5   71     9  15 1973-09-15
## 139    46     237  6.9   78     9  16 1973-09-16
## 140    18     224 13.8   67     9  17 1973-09-17
## 141    13      27 10.3   76     9  18 1973-09-18
## 142    24     238 10.3   68     9  19 1973-09-19
## 143    16     201  8.0   82     9  20 1973-09-20
## 144    13     238 12.6   64     9  21 1973-09-21
## 145    23      14  9.2   71     9  22 1973-09-22
## 146    36     139 10.3   81     9  23 1973-09-23
## 147     7      49 10.3   69     9  24 1973-09-24
## 148    14      20 16.6   63     9  25 1973-09-25
## 149    30     193  6.9   70     9  26 1973-09-26
## 150    NA     145 13.2   77     9  27 1973-09-27
## 151    14     191 14.3   75     9  28 1973-09-28
## 152    18     131  8.0   76     9  29 1973-09-29
## 153    20     223 11.5   68     9  30 1973-09-30

Geometric Objects

• Geometric objects are use to represent data or statistical transformations of the data.
• We are already familiar with many common geometric objects.
  • Boxes used in boxplots
  • Bins used in histograms
  • Bars used in barchart
  • Points in a scatter plot
  • Lines in a line chart

Mapping Aesthetics

• Properties of geometric objects, such as points, lines, colours, and shapes, are referred to as aesthetics
• The process of assigning variables from a dataset to aesthetics is known as mapping.
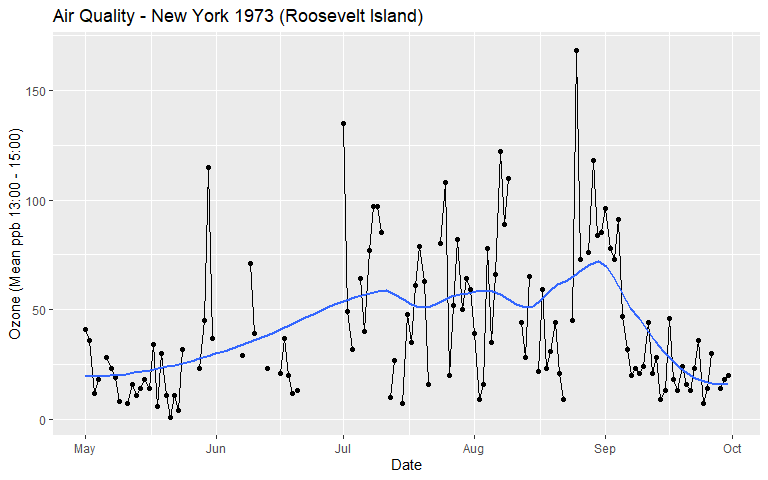
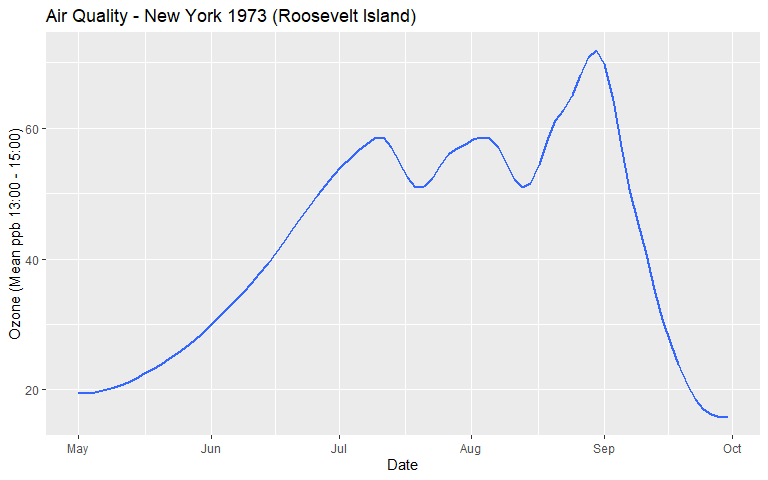
• For example in the air quality example x = Date and y = Ozone.
• Points are geometric objects and the position they are drawn on the plot is determined by the mappings.

geoms vs aes

Statistical Transformations

• Many visualisations use statistical summaries of the raw data.
• Examples of stats transformations include the following:
  • quartiles of box plots
  • means
  • error bar/confidence intervals
  • binning in histograms and dot plots
  • tallies, counts, proportions, percentages in bar charts
  • lines of best fit for linear regression.
• Statistical transformations are the reason why statistics is so important for data visualisation.

Statistical Transformations Cont.

• The smoothed trend line in the Air Quality visualisation was estimated using a non-parametric, locally weighted regression model

Scales

• Scales are used to control the mapping between a variable and an aesthetic.
• For example, changing the range of the x axis, or changing the colour of a colour scale.

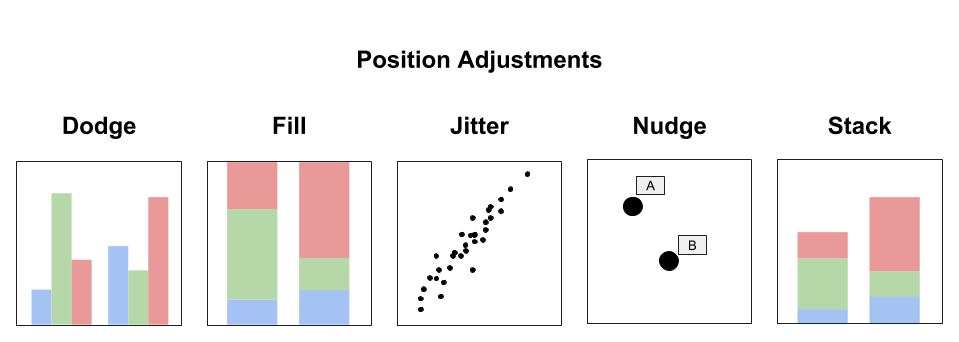
Position Adjustment

• Position adjustments aim to avoid overlapping elements by either dodging, filling, jittering, nudging or stacking. Layers can incorporate multiple position adjustments.

Coordinate System

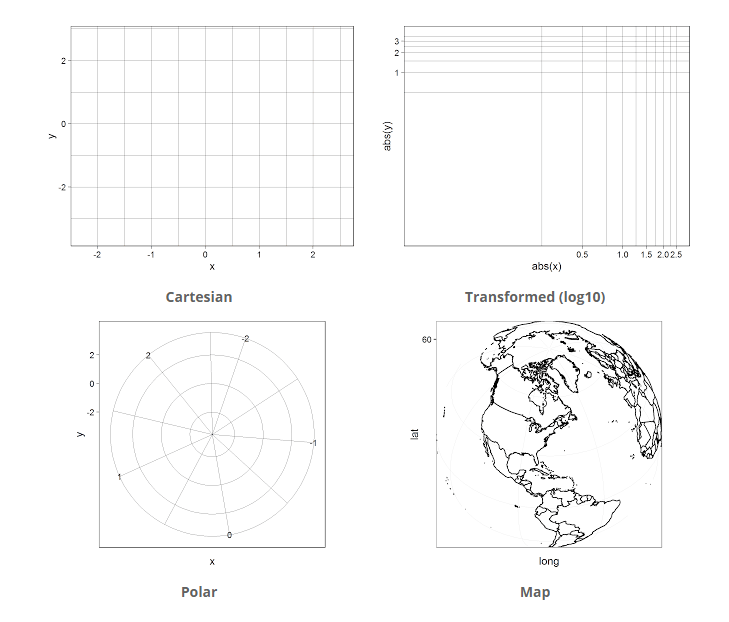
• Coordinate systems are used to determine the placement of geometric objects within a plot:

  • Cartesian
  • Transformed
  • Polar
  • Map

Faceting

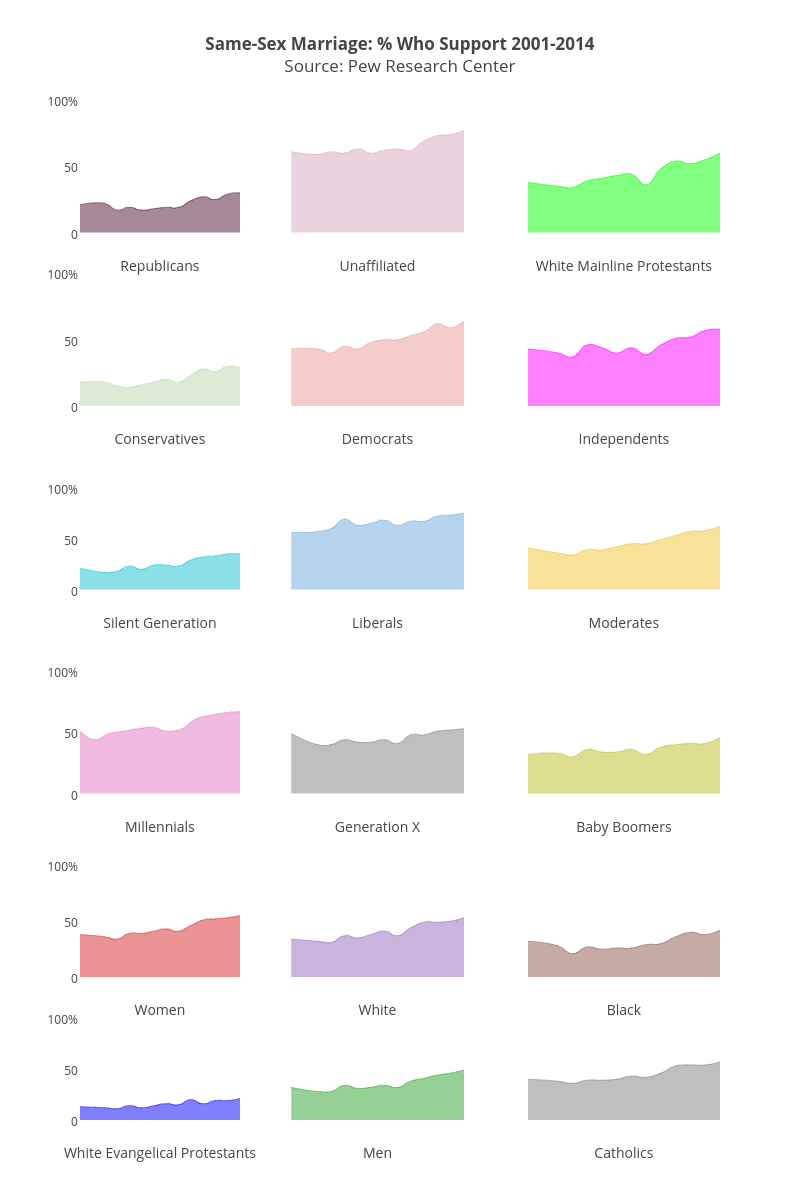
• Faceting is a powerful way to break a data visualisation into small multiples. This process is also known as latticing or trellising.

ggplot2

• ggplot2 is a high-level R package, developed by Hadley Wickham based on Layered Grammar of Graphics
• Why is it import to learn ggplot2?
  • Develop a basic but powerful grammar for building visualisations
  • Learn how to build visualisations layer by layer
  • Helps promote good practice in data visualisation - sensible defaults and colour use
  • Powerful and fully customisable

gglot2 - A Verbose Example

• Let’s take a look at how ggplot2 builds a visualisation.

install.packages("ggplot2")
library(ggplot2)

• We begin by creating a ggplot2 object, defining a coordinate system and selecting our scales.

ggplot() +
  coord_cartesian() +
  scale_x_date(name = "Date") +
  scale_y_continuous(name = "Ozone (Mean ppb 13:00 - 15:00)")

• And the result…

gglot2 - A Verbose Example Cont.

• Nothing because we have not defined any layers.

gglot2 - A Verbose Example Cont. 2

• Let’s add a layer for points…

ggplot() +
  coord_cartesian() +
  scale_x_date(name = "Date") +
  scale_y_continuous(name = "Ozone (Mean ppb 13:00 - 15:00)") +
  layer(
    data = airquality,
    mapping = aes(x = date, y = Ozone),
    stat = "identity",
    geom = "point",
    position = position_identity()
  )

gglot2 - A Verbose Example Cont. 3

• Now we are getting somewhere…

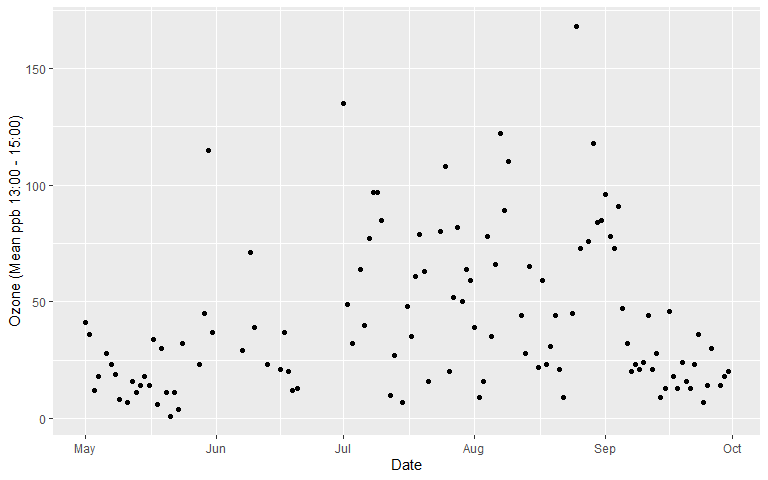
gglot2 - A Verbose Example Cont. 4

• Now for the lines…

ggplot() +
  coord_cartesian() +
  scale_x_date(name = "Date") +
  scale_y_continuous(name = "Ozone (Mean ppb 13:00 - 15:00)") +
  layer(
    data = airquality,
    mapping = aes(x = date, y = Ozone),
    stat = "identity",
    geom = "point",
    position = position_identity()
  ) +
  layer(
    data = airquality,
    mapping = aes(x = date, y = Ozone),
    stat = "identity",
    geom = "line",
    position = position_identity()
  )

gglot2 - A Verbose Example Cont. 5

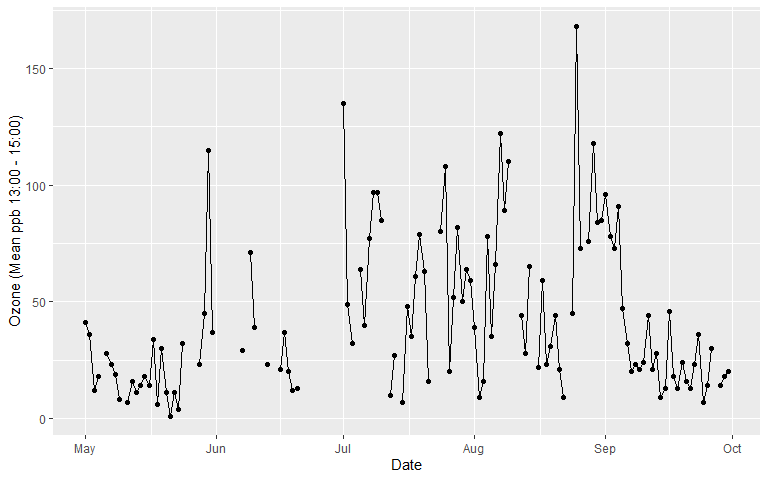
gglot2 - A Verbose Example Cont. 6

• And the trend line…

ggplot() +
  coord_cartesian() +
  scale_x_date(name = "Date") +
  scale_y_continuous(name = "Ozone (Mean ppb 13:00 - 15:00)") +
  layer(
    data = airquality,
    mapping = aes(x = date, y = Ozone),
    stat = "identity",
    geom = "point",
    position = position_identity()
  ) +
  layer(
    data = airquality,
    mapping = aes(x = date, y = Ozone),
    stat = "identity",
    geom = "line",
    position = position_identity()
  ) +
  layer(
    data = airquality,
    mapping = aes(x = date, y = Ozone),
    stat = "smooth",
    params = list(method = "loess", span = 0.4, se = FALSE),
    geom = "smooth",
    position = position_identity()
  )

gglot2 - A Verbose Example Cont. 7

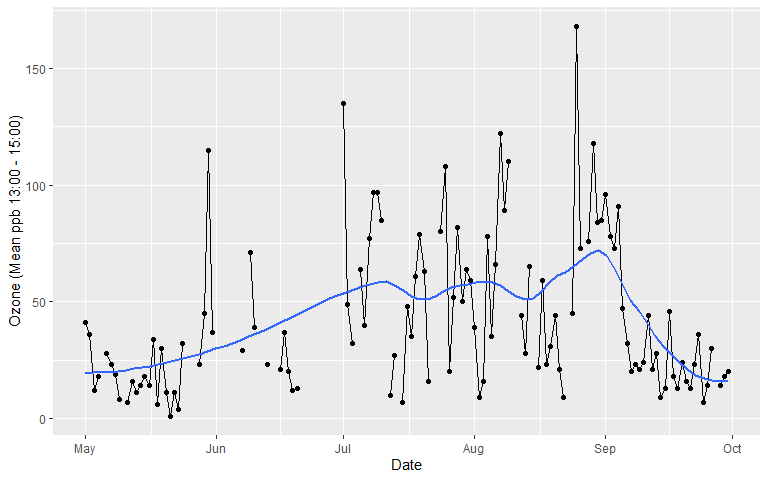
gglot2 in Practice

• That was a lot of code!
• In practice, ggplot2 is far more succinct.
• The following code will reproduce the same visualisation

p <- ggplot(data = airquality, aes(x = date, y = Ozone))
p + geom_point() +
  geom_line(aes(group = 1)) +
  geom_smooth(se = FALSE, span = 0.4) +
  labs(
    title = "Air Quality - New York 1973 (Roosevelt Island)",
    x = "Date",
    y = "Ozone (Mean ppb 13:00 - 15:00)"
    )

• Let’s take a closer look at more efficient ways to code ggplot2.

Demo Data - Student Alcohol Survey

• A survey of 649 Portuguese students aged 15 to 22.
• Questions related to alcohol consumption, demographics, family background, academic and social factors.
• A clean copy of the data can be downloaded here.
• The original data was downloaded from the UCI Machine Learning Repository

student <- read.csv("../data/Student_alcohol_survey.csv")

qplot()

• The qplot() function in ggplot2 is a quick method to develop basic data visualisations with sensible defaults.

qplot(x = Fjob, data = student, geom = "bar")

qplot() cont.

• Box plot:

qplot(x = Fjob, y = G3, data = student, geom = "boxplot")

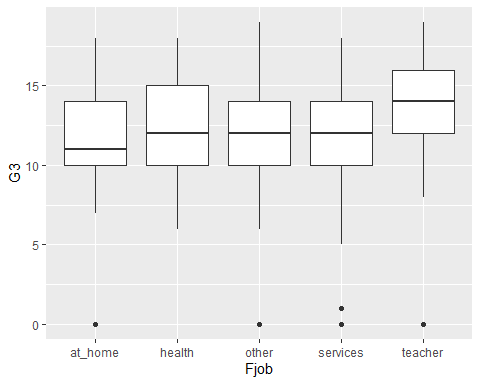
qplot() cont. 2

• Add some markers for the mean:

qplot(x = Fjob, y = G3, data = student ,geom = "boxplot") +
  stat_summary(fun.y = mean, colour = "red", geom = "point")

qplot() cont. 3

• A basic scatter plot:

qplot(x = G1, y = G3, data = student, geom = "point")

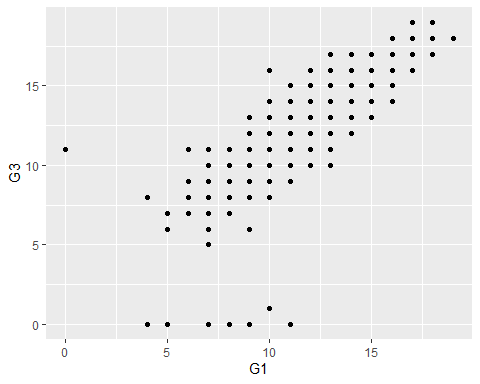
qplot() cont. 4

• Add a line of best fit based on a linear model:

qplot(x = G1, y = G3, data = student, geom = "point") +
  geom_smooth(method = "lm")

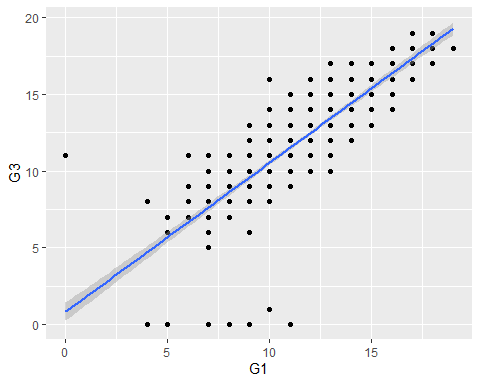
qplot() cont. 5

• A scatter plot with a colour mapped to sex:

qplot(x = G1, y = G3, data = student, colour = sex, geom = "point")

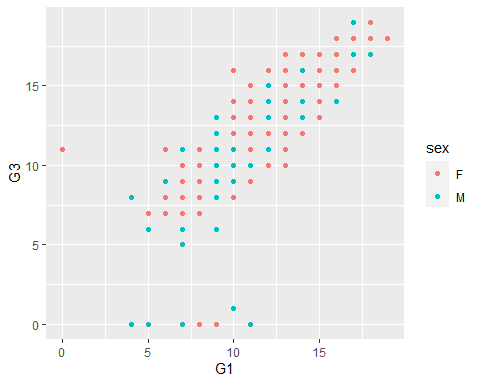
qplot() cont. 6

• Add individual lines of best fit for each factor level mapped to the colour aesthetic:

qplot(x = G1, y = G3, data = student, colour = sex, geom = "point") +
  geom_smooth(method = "lm")

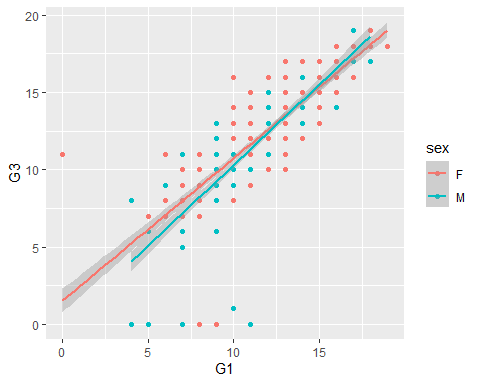
qplot() cont. 7

• Facet scatter plots by mother’s job:

qplot(x = G1,y = G3, data = student, geom = "point") +
  geom_smooth(method="lm") + facet_wrap(~ Mjob)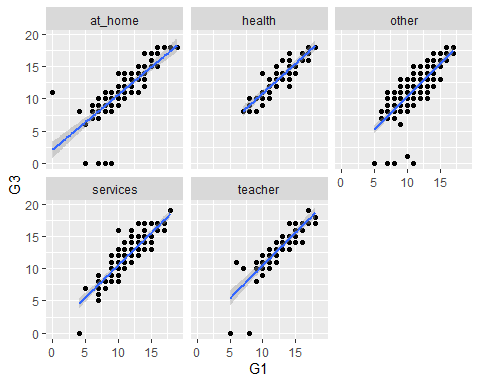

ggplot()

• ggplot() is a more powerful, layered approach to building a visualisation.
• Let’s create a simple box plot comparing final grades by alcohol use ratings (1 - 5)
• First we define a ggplot object, p1

p1 <- ggplot(data = student, mapping = aes(x = as.factor(Dalc), y = G3))

• aes are the aesthetic mappings. Any layers added will map the data to the corresponding aesthetics in the geom. For example, a box plot.

ggplot() cont.

p1 + geom_boxplot()

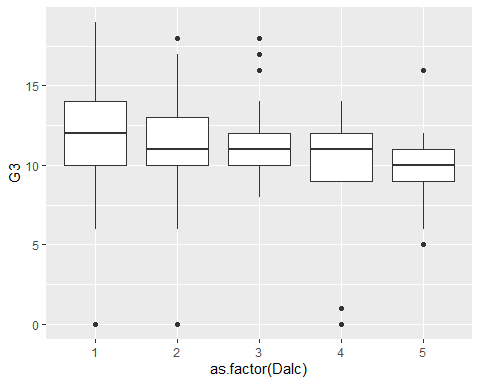
• Now we can continue to use p1 to add more layers or change the visualisation completely.

ggplot() cont. 2

• We can map additional variables to other scales…
• Note how we mapped a fill aesthetic to sex.

p2 <- ggplot(student, aes(x = as.factor(Dalc), y = G3, fill = sex))
p2 + geom_boxplot()

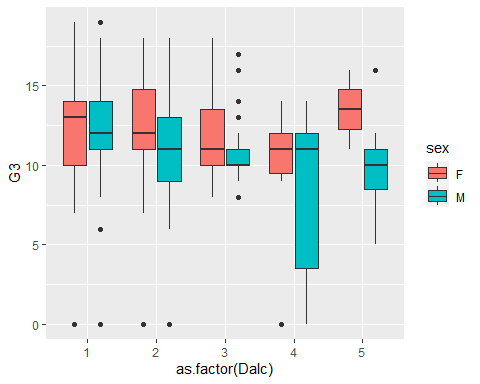
ggplot() cont. 3

• Box plots hide sample size. Use a different geom that conveys sample size…

p3 <- ggplot(student, aes(x = as.factor(Dalc), y = G3, colour = sex))
p3 + geom_point()

ggplot() cont. 4

• Note colour refers to the outline or solid colour of an object. fill refers to the inside colour of a large object, e.g. bar or box.

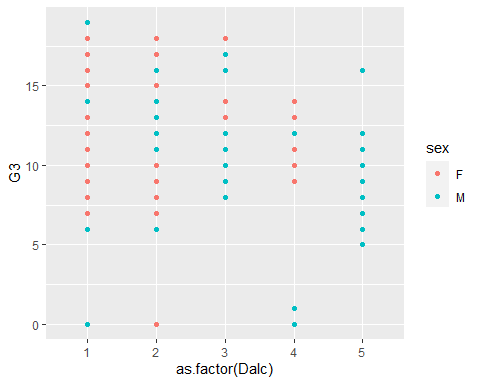
ggplot() Jitter

• Points and categories overlap!
• Use position adjustments to avoid over-plotting

p3 + geom_jitter(position = position_jitterdodge())

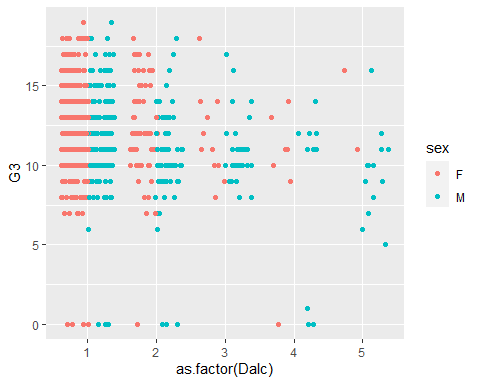
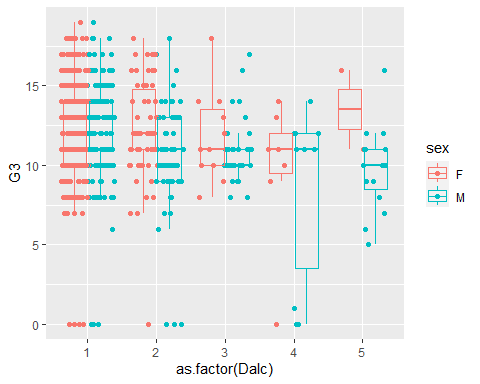
ggplot() Adding Layers

• Overlaying additional geoms is easy…
• Note how we use outlier.shape = NA to suppress the outliers plotted for the boxplot

p3 + geom_jitter(position = position_jitterdodge()) +
  geom_boxplot(fill = NA, outlier.shape = NA)

ggplot() Themes

• You can change default themes:

p3 + geom_jitter(position = position_jitterdodge()) +
  geom_boxplot(fill = NA, outlier.shape = NA) + theme_bw()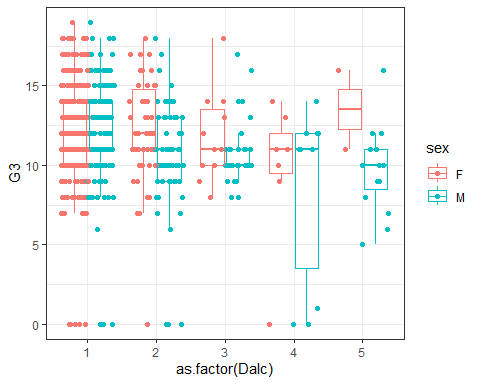

ggplot() Adding Titles and Labels

• You can define descriptive labels:

p3 + geom_jitter(position = position_jitterdodge()) +
  geom_boxplot(fill = NA, outlier.shape = NA) +
  labs(title = "Final Grades by Gender and Alcohol Consumption Ratings",
       x = "Weekday Alcohol Consumption Rating (1 = low - 5 = high)",
       y = "Final Grade - Portuguese")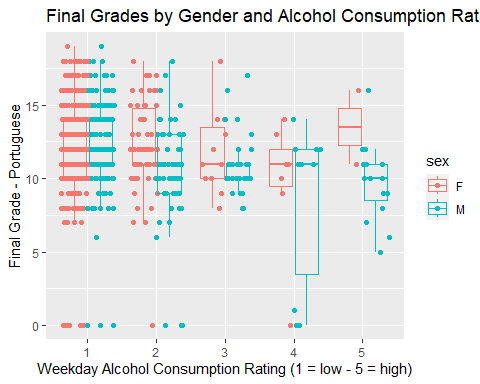

ggplot() Saving

• You can use RStudio to save and export your data visualisation as an image (PNG, JPG, TIFF, BMP, Metafile, SVG and EPS), PDF or to the clipboard.
• You can also use the nifty ggsave() function which saves an image, using sensible defaults, to your working directory.

ggsave("Box_plot_Grades_Gender_Consumption_01.png",
       width = 18, height = 12, units = "cm")

• You might have to play around with the width and height. Measurements are in inches by default. You need to specify "cm" if you want metric.

Colour in R

<img src=“../images/brewer.png” width=“30%”, align = “right”>

• R allows colour assignment using a few different methods:
  • Colour code models: For example, hexadecimal codes as well as others including HSV, HSL, RGB and CMYK.
  • Inbuilt R colour names (657 to choose from)
  • Packages such as RColorBrewer

colourpicker

<img src=“../images/colourpickerdemo.PNG” width=“30%”, align = “right”>

• The colourpicker package provides ggplot2 with a very useful interface for colour picking and exploration.

• First, install the package.

install.packages("colourpicker")

• Now, load the package.

library(colourpicker)

• You can access the Colour Picker through the Addins menu in RStudio

Basic Colour Assignment

• Produce a histogram showing the distribution of pizza diameter.

Pizza <- read.csv("../data/Pizza.csv")
p1 <- ggplot(data = Pizza, aes(x = Diameter))
p1 + geom_histogram()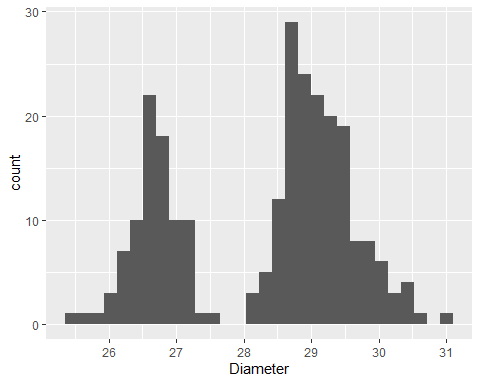

Basic Colour Assignment Cont.

• Change colour using R colour names

p1 + geom_histogram(fill = "dodgerblue", colour = "black")

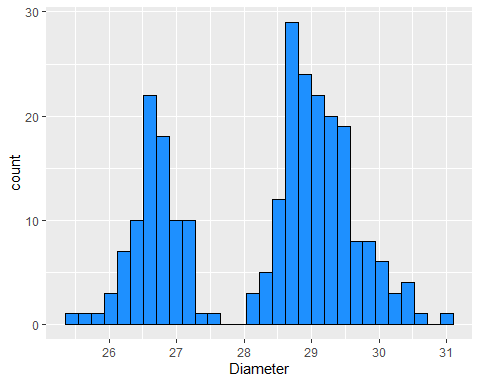
Basic Colour Assignment Cont. 2

• Change colour using hex codes

p1 + geom_histogram(fill = "#ff0066", colour = "#000000")

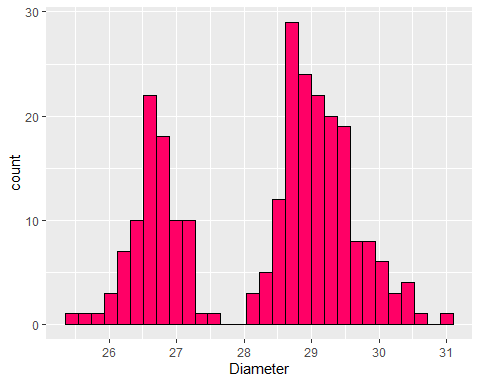
Colour Scales

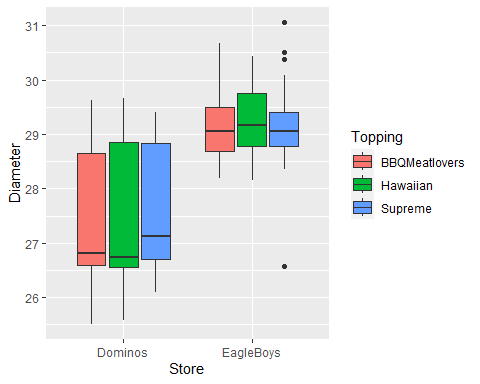
Nominal Colour Scale Example

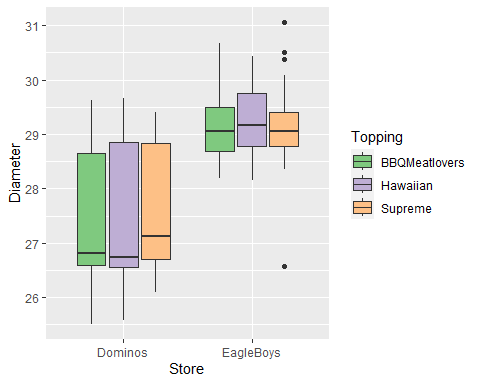
• Side-by-side box plot comparing pizza diameter by Store and Topping

p2 <-ggplot(data = Pizza, aes(x = Store, y = Diameter, fill = Topping))
p2 + geom_boxplot()

Nominal Colour Scale Example Cont.

• Change ColourBrewer palette…

p2 + geom_boxplot() + scale_fill_brewer(palette = "Accent")

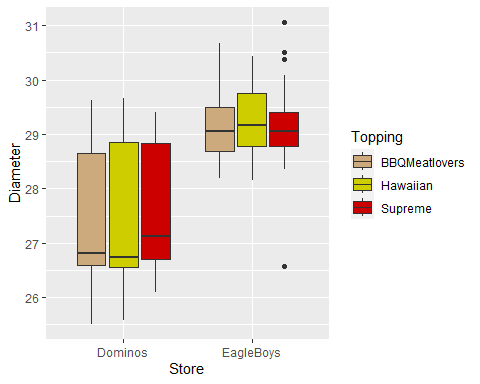
Nominal Colour Scale Example Cont. 2

• Set manual colour scale…

p2 + geom_boxplot() + scale_fill_manual(
  values = c("burlywood3","yellow3","red3"))

Ordinal Colour Scale Example

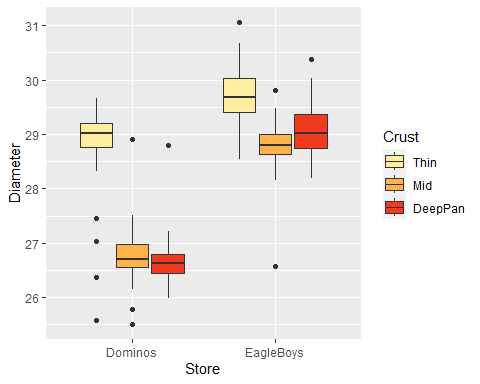
• Boxplot comparing pizza diameter by Store and Crust.

Pizza$Crust<-factor(Pizza$Crust, levels = c("Thin","Mid","DeepPan"),
                    ordered = T)
p3 <-ggplot(data = Pizza, aes(x = Store, y = Diameter, fill = Crust))
p3 + geom_boxplot()

Ordinal Colour Scale Example Cont.

• Change palette()…

p3 + geom_boxplot() + scale_fill_brewer(palette = "YlOrRd")

Continuous Colour Scale

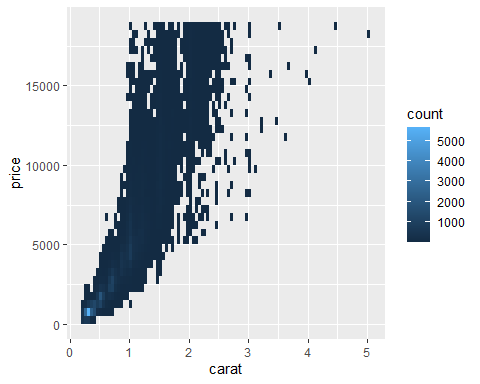
• Explore the relationship between diamond carat and price

Diamonds <- read.csv("../data/Diamonds.csv")
p4 <- ggplot(data = Diamonds, aes(x = carat, y = price))
p4 + geom_point()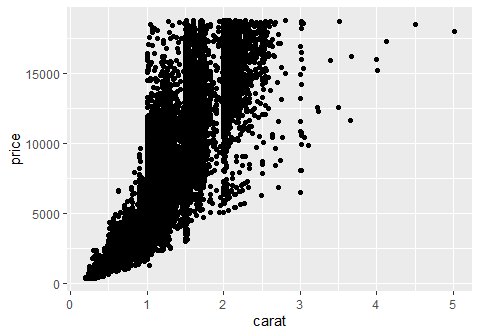

• Hard to see data density as \(n = 53940\).

Continuous Colour Scale Cont.

• Use a continuous colour scale to represent data density in a 2d histogram

p4 + geom_bin2d(binwidth = c(0.05, 500))

Continuous Colour Scale Cont. 2

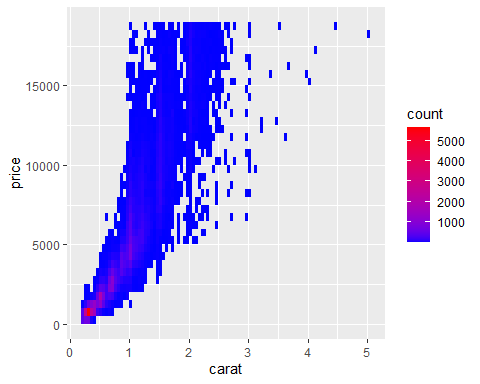
• Change colour gradient…

p4 + geom_bin2d(binwidth = c(0.05, 500)) +
  scale_fill_gradient(low="blue", high="red")

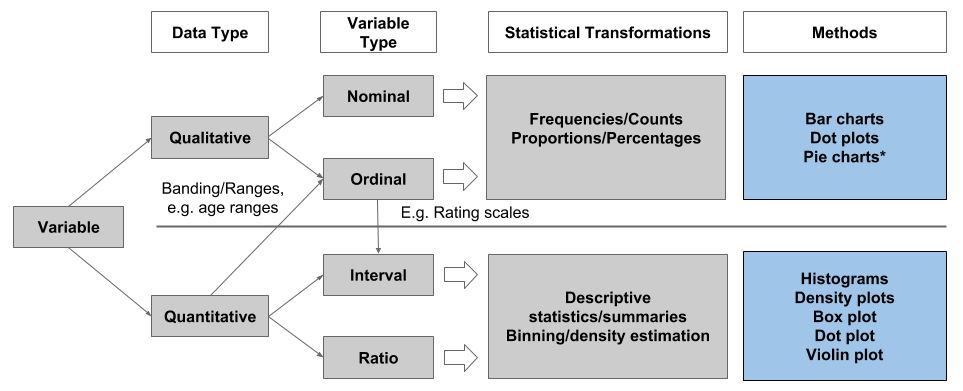
Overview - Common Univariate Methods

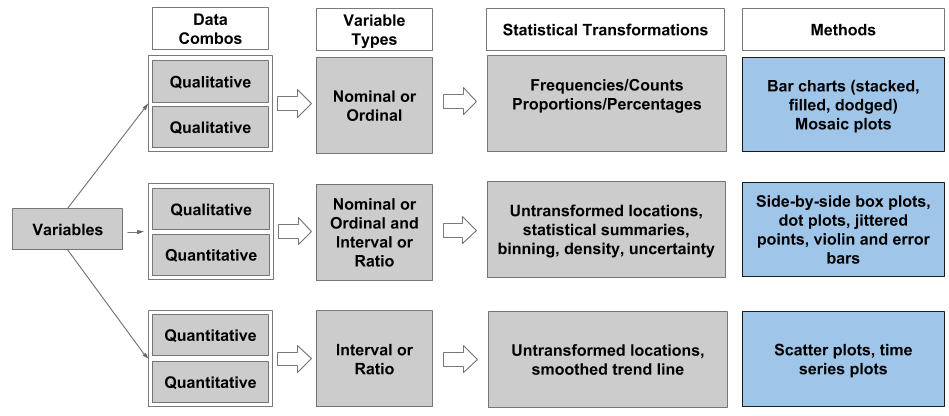
Overview - Common Bivariate Methods

ggplot2 Resources

• Recommended resources:
  • ggplot2 Documentation
  • ggplot2: Elegant Graphics for Data Analysis
  • Data Visualisation with ggplot2 Cheat Sheet
  • Read Hadley’s Wickham’s paper - A Layered Grammar of Graphics